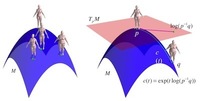
Top row: Body manifold. Left: Human shapes as points on a manifold, M. Every point represents a deformation from a template. Center: Distance between shapes p and q is measured via a geodesic distance; i.e. the length of the path between them along M. Right: The tangent space at p, denoted by TpM, is a vector space.
Three-dimensional object shape is commonly represented in terms of deformations of a triangular mesh from an exemplar shape. In particular, statistical generative models of human shape deformation are widely used in computer vision, graphics, ergonomics, and anthropometry. Existing models, however, are based on a Euclidean representation of shape deformations. In contrast, we argue that shape has a manifold structure: For example, averaging the shape deformations for two people does not necessarily yield a deformation corresponding to a valid human shape, nor does the Euclidean difference of these two deformations provide a meaningful measure of shape dissimilarity. Consequently, we define a novel manifold for shape representation, with emphasis on body shapes, using a new Lie group of deformations. This has several advantages.
First, we define triangle deformations exactly, removing non-physical deformations and redundant degrees of freedom common to previous methods.
Second, the Riemannian structure of Lie Bodies enables a more meaningful definition of body shape similarity by measuring distance between bodies on the manifold of body shape deformations.
Third, the group structure allows the valid composition of deformations. This is important for models that factor body shape deformations into multiple causes or represent shape as a linear combination of basis shapes. Similarly, interpolation between two mesh deformations results in a meaningful third deformation.
Finally, body shape variation is modeled using statistics on manifolds. Instead of modeling Euclidean shape variation with Principal Component Analysis we capture shape variation on the manifold using Principal Geodesic Analysis.
Our experiments show consistent visual and quantitative advantages of Lie Bodies over traditional Euclidean models of shape deformation and our representation can be easily incorporated into existing methods.
This project is part of a larger effort that brings together statistics and geometry to model statistics on manifolds. Our research on manifold-valued statistics addresses the problem of modeling statistics in constrained feature spaces. We try to find the geometrically most natural representations that respect the constraints; e.g. by modeling the data as belonging to a Lie group or a Riemannian manifold. We take a geometric approach as this keeps the focus on good distance measures, which are essential for good statistics.
2 Technical University of Denmark