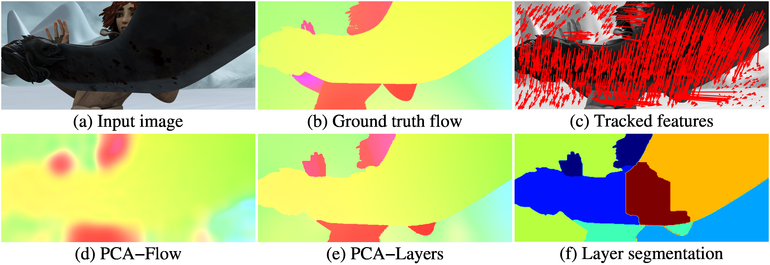
Results of the proposed algorithms. In a pair of input images (a), sparse features are matched (c) and interpolated using a learned basis, yielding an approximate optical flow field (d), the result of PCA-Flow. Using a layered formulation, PCA-Layers, the accuracy can be significantly increased (e). (f) shows the extracted segments. (b) shows the ground truth optical flow.
PCA Flow
Jonas Wulff,
Michael J. Black
Despite decades of research, a fast optical flow algorithm, that is also accurate, remains an elusive goal. While recent optical flow methods such as DeepFlow are highly accurate, for many applications speed is often as important. Most current methods take several seconds (or minutes) per frame, making them impractical for long sequences. The fastest optical flow algorithms run in under a second, but rely on GPUs, which are not available on all platforms. We address both accuracy and speed and propose a new approach called PCA-Flow that is based on sparse feature matches followed by interpolation. Both steps are fast to compute. To increase accuracy, especially at motion boundaries, we extend PCA-Flow to a layered framework. Both approaches are significantly faster than methods with comparable accuracies.
PCA-Flow
The basic assumption for our work is that an arbitrary optical flow field can be approximated as a weighted sum of a small number of basis flow fields. Previously such linear flow models were only used in small image patches or simple, inherently low-dimensional scenarios such as driving vehicles. In contrast, we use a linear model for full-frame optical flow in arbitrary scenes. To find a suitable basis, we first compute optical flow for four Hollywood movies, resulting in 8 hours of flow data. We then compute the basis that spans this optical flow using a robust PCA method, and take the first 250 eigenvectors in both horizontal and vertical directions as the basis vectors.
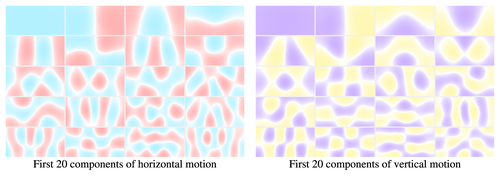
A linear model has three main advantages. First, given a fixed basis, the optical flow field is completely determined by the weights, yielding a much more compact representation than the 2D vector field. Second, a domain-specific prior (for example for automotive scenarios) on the weights can be learned even from small training sets. Third, given sparse, matched features and taking the prior into account, we can efficiently compute the weights as the solution to a robustified, Tikhonov-regularized least squares problem.
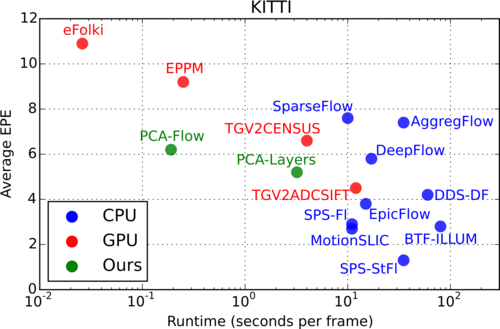
The title image shows an example for an optical flow field computed by PCA-Flow. Due to the low dimensionality of the optical flow basis, motion boundaries are blurry. However, in terms of average endpoint error our method beats the widely used methods Classic+NL and LDOF, while requiring on average 190 ms per flow field on a CPU. The accuracy / runtime tradeoff becomes obvious in a comparison of PCA-Flow and other state of the art algorithms in the accuracy/runtime plane on KITTI. While many algorithms are more accurate than ours, they are all several times slower.
PCA-Layers
To increase accuracy at the motion boundaries, we extend PCA-Flow to a layered model, PCA-Layers. This assumes that an optical flow field can be decomposed into segments, each containing very simple motion. Unfortunately so far, layered models have been computationally expensive. Here, we cluster matched features into layers using Expectation Maximization (EM), and use PCA-Flow to efficiently compute the motion of each layer. The computation of a dense flow field then becomes a labelling problem, in which each pixel is assigned to one of the motion layers. We formulate this as a Markov Random Field, taking into account brightness constancy, color consistency and spatial compactness within the layers, and a smoothness term that incorporates image content. This smoothness term leads to good extrapolation of flow values to image regions that are not well covered by matched features.
The title image shows an example for the computed layer segmentation and the resulting optical flow. Compared to PCA-Flow, the motion boundaries are much better preserved. PCA-Layers takes on average 3.2 seconds per pair of frames, and in MPI-Sintel ranks in place 10 of 36 in the final pass and in place 9 of 36 in the clean pass, beating popular methods such as MDP-Flow. The next fastest method with similar accuracy, SparseFlow, is over 2.5 times slower, taking 10 s per frame.

The code and documentation is on Github.
The learned basis and the learned covariance matrices for Sintel and KITTI can also be downloaded separately.